Algebraic Expressions (Monomials & Polynomials), Conformation, Fundamental Operations.

In this publication I will be highlighting the importance of algebraic expressions of monomial and polynomial types, some important operations that are carried out in any area of human development, especially in the scientific field.

Let’s begin then to decipher this language and go arming some algebraic expressions, highlighting that the most important feature is the generality that we obtain at the moment of its implementation, that is, when we manage to formulate an approach or statement through the use of letters or symbols, we are in the presence of an algebraic expression, which will help us to solve this approach like any other similar characteristics, in more practical terms.

It is important to know how we can structure or conform a certain expression of monomial or polynomial type, through a practical activity that we can observe in our environment, in it we find innumerable phenomena studied by science through the structuring and application of monomial or polynomial expressions, therefore we observe objects or figures that for their respective study need to know on a specific occasion the total area at atomic, molecular or system levels in general.

Development or conformation of a monomial expression

Through a practical and general exercise known to all, we will use the geometric figure called cube, if we wanted to know the total area for any cube regardless of its size, we can do it using a general formulation, that is, a monomial or polynomial algebraic expression:

When deploying this geometric figure, we notice the yes (6) square sides that make it up, therefore the measurements of each side of one of its faces are exactly symmetrical or equal, so for the area of each face we represent it with the variable x raised to exponent 2, to know the total area of all its sides we have the following monomial expression:

Elaboration or conformation of a polynomial expression

But if we want to do the same to know the total area of a straight prism with square base and edges of lengths x, y; therefore, for your total area we have:

In this way we obtain the polynomial expression:

With these two examples we give way to formulations of monomial and polynomial expressions, one of the fundamental bases for the consolidation of other knowledge such as equations, graphs and functions also very useful for the field of science in all areas, points that in other publications I will be expanding.

Now it is important to know or deepen on some aspects or fundamental characteristics of both monomials and polynomials:

Fundamental aspects

Monomies

Expressions like 6×2, 4xy o 2×2, which we obtained in the previous examples are called monomials, these are formed by a literal part and a numerical part they represent the following:

It is very important to remember that the first letters of the alphabet are used to designate coefficients, while the last letters we use to represent the variables of a certain monomial type algebraic expression for this case, for example:

If we have the expression 5ax, the coefficient will be 5a while the variable is the Literal x, because in this case the literals (a) and (X) do not represent things of the same type, because the letter (a) represents a fixed or constant value, although we do not specify what that value is, while the literal or letter x can represent any value.

It is important to note that sometimes some confuse the expression of the monomial, this is because the mono prefix is related to a single term, which is true but for example:

Although this term is composed of a number, three variables and an exponent, they all represent a single expression, since when giving values to the variables the result will be a single quantity, that is, consider giving values to the three variables, for x=2; y=3; z=1

We would have then:

Degree of a monomial

When we are in the presence of a monomial, the degree of it is determined by the sum of the exponents to which the variables are elevated, whether they are of the same type of literal or not, for example:

Monomials with variables represented with the same literal or letter, in this case the x.

But we also have cases of monomials of degree two with the following characteristics:

This complies with the above, we add the exponents of the variables despite being represented by different or different letters, that is, both x and y are raised to 1, therefore 1 + 1 = 2, this will determine the degree of said monomial.

Another example of this type:

Recall that when we are in the presence of a coefficient which does not represent the product with any variable its degree is considered = 0.

Polynomials

Polynomials are expressions formed by two or more monomials, usually we find polynomials of the type: 2x + 3xy, which we call binomial, and if we have 4yz + 6xz + 5xyz, we call it trinomials, this is due to the amount of monomials present in such expressions, two (2) for the first case and (3) for the second case, but the important thing is not to be confused, and be clear that from two terms we are in the presence of a polynomial, and the other denominations are particular cases for their identification, that is, types of polynomials.

Degree of a polynomial

For this case we are led by the largest of the degrees of the monomials that form this polynomial expression, example:

Expression whose variables are represented only by the literal or letter x.

Polynomial expression represented by variables whose literals are different:

Order of a polynomial

The polynomials are customarily written in an orderly manner, following the decreasing pattern of the exponents of the variables and with respect to said variables, example:

Now we express this same expression with respect and:

Then we order it with respect to the third variable that is used, that is, z:

We can highlight that a polynomial is complete as long as all the exponents appear in one of its variables consecutively, as for the first case.

Operations with monomials and polynomials

See Other Articles Others Are Reading

• History As A Science | What Makes History A Science
• Fire And Safety | Basic Fire Safety Tips & Fire Safety Rules
• Myths Surrounding Exercises | All You Need To Know Concerning Exercises.
• Criminal Profiling – Facts Over Fiction | Criminal Profiling Techniques
• 5 Tips For Students Who Are Considering Graphic Design As A Career.
• Evaluation Of Learning: How To Know If The Children Are Learning

Addition and subtraction of monomials

Addition and subtraction of polynomials

Product of polynomials

To solve the product of two polynomials we multiply term by term of one polynomial with the other and then add or subtract the same monomials according to the case with its variables:

Division of polynomials

Like the division of numbers, this type of operation can give exact or not, when it is not we consider that entire division, since it consists in the calculation of two polynomials, one called quotient polynomial and the other remains, therefore, we can affirm that the dividend has to be equal to the product of the divisor by the quotient, plus the rest.

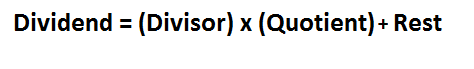
For the resolution of this type of division of polynomials of the same variable, we can consider as verification support two very important tools as represented by the rest theorem and the ruffini rule, both provide information that allow us to simplify this process or check the same.

Rest theorem

Through its application we can obtain the rest of the division of a polynomial by a binomial of the type (xa) or (x + a), with variables, therefore, it consists of taking the numerical value of the constant (a) changing it of sign and replace it in the variables x of a given polynomial, example: Given the following polynomials, divide P (x) by Q (x), apply the rest theorem:

In this way we can obtain the rest of the polynomial division, without the need to solve it, later we will develop the division as it is done to use the result of this theorem for its verification, before it is necessary to apply the other tool mentioned, that is, ruffini.

Ruffini’s Rule

Through this rule we can find both the quotient and the rest of a division of a polynomial by a binomial of the type (x – a) or (x + a), it consists of taking the coefficients of the polynomial P (x), then multiplying them with the value of the constant (a) of the binomial in question but changing it of sign, as shown in the figure below:

Now applied the two tools described above, ie, Theorem of the rest and Ruffini’s Rule proceed to the resolution of the division of the mentioned polynomials, with it we can verify if both the rest and quotient give us the same.

When solving this polynomial we verified that the application of both the theorem of the rest and Ruffini coincides with the results in this operation, both in the rest and in the quotient, therefore, we can use them for the verification of the three operations.

The abstract language is a broad and complex field which impacts on incalculable areas of human intellectual development, by means of monomial and polynomial expressions we can introduce ourselves to this wonderful world of abstraction, which will always be in permanent contact with the knowledge of our environment.

That’s the much we can take on the topic “Algebraic Expressions (Monomials & Polynomials), Conformation, Fundamental Operations.”.

Thanks For Reading

O3SCHOOLS TEAM